A Picture That Shows Space 2d Enclosed Area Art

Geometric space with four dimensions

The 4D equivalent of a cube is known as a tesseract, seen rotating hither in iv-dimensional space, even so projected into ii dimensions for display.

A iv-dimensional infinite (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Iii-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called dimensions, to draw the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is constitute by measuring and multiplying its length, width, and meridian (often labeled ten, y, and z).

The thought of adding a fourth dimension began with Jean le Rond d'Alembert'south "Dimensions" published in 1754,^{[1] [two]} was followed by Joseph-Louis Lagrange in the mid-1700s, and culminated in a precise formalization of the concept in 1854 past Bernhard Riemann. In 1880, Charles Howard Hinton popularized these insights in an essay titled "What is the Time?", which explained the concept of a "iv-dimensional cube" with a step-by-footstep generalization of the properties of lines, squares, and cubes. The simplest class of Hinton's method is to draw two ordinary 3D cubes in 2D space, one encompassing the other, separated past an "unseen" distance, and then draw lines between their equivalent vertices. This tin be seen in the accompanying animation whenever it shows a smaller inner cube inside a larger outer cube. The 8 lines connecting the vertices of the two cubes in this case represent a unmarried direction in the "unseen" quaternary dimension.

Higher-dimensional spaces (i.e., greater than three) have since get 1 of the foundations for formally expressing modern mathematics and physics. Large parts of these topics could not exist in their electric current forms without the use of such spaces. Einstein's concept of spacetime uses such a 4D space, though it has a Minkowski structure that is slightly more complicated than Euclidean 4D space.

Unmarried locations in 4D space can be given equally vectors or n-tuples, i.eastward. as ordered lists of numbers such as (x, y, z, w). Information technology is only when such locations are linked together into more complicated shapes that the full richness and geometric complexity of higher-dimensional spaces sally. A hint to that complexity can be seen in the accompanying 2nd animation of one of the simplest possible 4D objects, the tesseract (equivalent to the 3D cube; come across also hypercube).

History [edit]

Lagrange wrote in his Mécanique analytique (published 1788, based on work done effectually 1755) that mechanics can be viewed every bit operating in a four-dimensional space — three dimensions of space, and one of time.^[3] In 1827 Möbius realized that a time would let a three-dimensional class to be rotated onto its mirror-image,^{[4] : 141} and by 1853 Ludwig Schläfli had discovered all the regular polytopes that exist in higher dimensions, including the four-dimensional analogues of the Platonic solids, but his work was non published until after his death.^{[4] : 142–143} Higher dimensions were soon put on business firm footing by Bernhard Riemann's 1854 thesis, Über die Hypothesen welche der Geometrie zu Grunde liegen, in which he considered a "bespeak" to be any sequence of coordinates (x ₁, ..., 10 _n ). The possibility of geometry in higher dimensions, including four dimensions in particular, was thus established.

An arithmetics of 4 dimensions chosen quaternions was defined by William Rowan Hamilton in 1843. This associative algebra was the source of the science of vector analysis in three dimensions as recounted in A History of Vector Assay. Soon after tessarines and coquaternions were introduced equally other iv-dimensional algebras over R.

1 of the kickoff major expositors of the fourth dimension was Charles Howard Hinton, starting in 1880 with his essay What is the Fourth Dimension?; published in the Dublin University magazine.^[5] He coined the terms tesseract, ana and kata in his book A New Era of Thought, and introduced a method for visualising the fourth dimension using cubes in the book Time.^{[6] [vii]}

Hinton's ideas inspired a fantasy near a "Church of the Fourth Dimension" featured by Martin Gardner in his Jan 1962 "Mathematical Games cavalcade" in Scientific American. In 1886 Victor Schlegel described^[8] his method of visualizing four-dimensional objects with Schlegel diagrams.

In 1908, Hermann Minkowski presented a paper^[9] consolidating the part of time as the fourth dimension of spacetime, the basis for Einstein'south theories of special and general relativity.^[10] But the geometry of spacetime, being non-Euclidean, is profoundly unlike from that explored by Schläfli and popularised by Hinton. The written report of Minkowski space required new mathematics quite different from that of four-dimensional Euclidean space, and so developed along quite different lines. This separation was less articulate in the popular imagination, with works of fiction and philosophy blurring the distinction, so in 1973 H. S. M. Coxeter felt compelled to write:

Niggling, if anything, is gained past representing the quaternary Euclidean dimension as fourth dimension. In fact, this idea, so attractively developed by H. G. Wells in The Time Automobile, has led such authors as John William Dunne (An Experiment with Time) into a serious misconception of the theory of Relativity. Minkowski'due south geometry of infinite-time is not Euclidean, and consequently has no connection with the present investigation.

Vectors [edit]

Mathematically, 4-dimensional space is a infinite with four spatial dimensions, that is a space that needs four parameters to specify a point in it. For example, a full general indicate might accept position vector a, equal to

${\displaystyle \mathbf {a} ={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\\a_{4}\end{pmatrix}}.}$

This can exist written in terms of the four standard basis vectors (e ₁, e _two, e ₃, eastward _iv), given by

${\displaystyle \mathbf {eastward} _{1}={\brainstorm{pmatrix}1\\0\\0\\0\end{pmatrix}};\mathbf {e} _{2}={\begin{pmatrix}0\\1\\0\\0\finish{pmatrix}};\mathbf {e} _{3}={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\mathbf {e} _{four}={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}},}$

so the general vector a is

${\displaystyle \mathbf {a} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{ii}+a_{iii}\mathbf {e} _{three}+a_{4}\mathbf {east} _{four}.}$

Vectors add, subtract and scale as in 3 dimensions.

The dot product of Euclidean three-dimensional infinite generalizes to four dimensions as

${\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{i}b_{1}+a_{two}b_{two}+a_{iii}b_{iii}+a_{4}b_{4}.}$

It can exist used to calculate the norm or length of a vector,

${\displaystyle \left|\mathbf {a} \correct|={\sqrt {\mathbf {a} \cdot \mathbf {a} }}={\sqrt {a_{1}^{2}+a_{two}^{2}+a_{iii}^{2}+a_{4}^{2}}},}$

and calculate or ascertain the bending between two non-zero vectors as

${\displaystyle \theta =\arccos {\frac {\mathbf {a} \cdot \mathbf {b} }{\left|\mathbf {a} \right|\left|\mathbf {b} \right|}}.}$

Minkowski spacetime is four-dimensional space with geometry defined by a non-degenerate pairing different from the dot product:

${\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{ane}b_{i}+a_{ii}b_{2}+a_{3}b_{iii}-a_{four}b_{4}.}$

As an example, the altitude squared between the points (0,0,0,0) and (1,1,1,0) is 3 in both the Euclidean and Minkowskian 4-spaces, while the distance squared between (0,0,0,0) and (one,1,1,ane) is four in Euclidean infinite and 2 in Minkowski space; increasing ${\displaystyle b_{iv}}$ actually decreases the metric altitude. This leads to many of the well-known apparent "paradoxes" of relativity.

The cross product is not defined in iv dimensions. Instead the exterior production is used for some applications, and is defined as follows:

${\displaystyle {\begin{aligned}\mathbf {a} \wedge \mathbf {b} =(a_{ane}b_{2}-a_{2}b_{1})\mathbf {eastward} _{12}+(a_{1}b_{iii}-a_{iii}b_{1})\mathbf {e} _{13}+(a_{1}b_{4}-a_{4}b_{1})\mathbf {e} _{14}+(a_{2}b_{3}-a_{3}b_{two})\mathbf {e} _{23}\\+(a_{2}b_{four}-a_{4}b_{2})\mathbf {e} _{24}+(a_{3}b_{4}-a_{4}b_{3})\mathbf {e} _{34}.\cease{aligned}}}$

This is bivector valued, with bivectors in four dimensions forming a six-dimensional linear space with basis (e ₁₂, eastward ₁₃, e ₁₄, east ₂₃, e ₂₄, eastward ₃₄). They tin can exist used to generate rotations in four dimensions.

Orthogonality and vocabulary [edit]

In the familiar three-dimensional space of daily life, there are three coordinate axes—usually labeled ten, y, and z—with each axis orthogonal (i.eastward. perpendicular) to the other two. The six cardinal directions in this space can exist called up, down, east, westward, north, and south. Positions forth these axes can be chosen altitude, longitude, and latitude. Lengths measured along these axes can be chosen height, width, and depth.

Comparatively, four-dimensional space has an actress coordinate centrality, orthogonal to the other three, which is usually labeled w. To depict the two additional cardinal directions, Charles Howard Hinton coined the terms ana and kata, from the Greek words meaning "up toward" and "down from", respectively^{[ citation needed ]}.

As mentioned above, Hermann Minkowski exploited the thought of four dimensions to hash out cosmology including the finite velocity of light. In appending a time dimension to three dimensional infinite, he specified an alternative perpendicularity, hyperbolic orthogonality. This notion provides his iv-dimensional infinite with a modified simultaneity appropriate to electromagnetic relations in his cosmos. Minkowski's world overcame bug associated with the traditional accented space and time cosmology previously used in a universe of three infinite dimensions and one time dimension.

Geometry [edit]

The geometry of 4-dimensional space is much more complex than that of three-dimensional space, due to the extra degree of freedom.

Just as in three dimensions there are polyhedra fabricated of two dimensional polygons, in four dimensions there are 4-polytopes made of polyhedra. In three dimensions, there are five regular polyhedra known as the Platonic solids. In four dimensions, there are 6 convex regular 4-polytopes, the analogues of the Platonic solids. Relaxing the atmospheric condition for regularity generates a farther 58 convex uniform 4-polytopes, coordinating to the xiii semi-regular Archimedean solids in 3 dimensions. Relaxing the conditions for convexity generates a farther 10 nonconvex regular 4-polytopes.

Regular polytopes in iv dimensions
(Displayed as orthogonal projections in each Coxeter aeroplane of symmetry)

A4, [3,3,3]	Biv, [4,iii,3]		F4, [3,4,three]	Hiv, [five,3,3]
5-cell {3,3,3}	tesseract {4,three,iii}	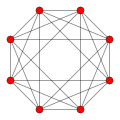16-cell {iii,3,iv}	24-cell {3,4,3}	600-cell {3,three,5}	120-cell {five,3,3}

In three dimensions, a circle may exist extruded to form a cylinder. In four dimensions, there are several different cylinder-like objects. A sphere may exist extruded to obtain a spherical cylinder (a cylinder with spherical "caps", known equally a spherinder), and a cylinder may be extruded to obtain a cylindrical prism (a cubinder).^{[ citation needed ]} The Cartesian product of two circles may be taken to obtain a duocylinder. All three can "roll" in four-dimensional space, each with its ain properties.

In 3 dimensions, curves can form knots just surfaces cannot (unless they are self-intersecting). In iv dimensions, withal, knots made using curves can be trivially untied by displacing them in the quaternary direction—only 2D surfaces tin can grade non-lilliputian, not-self-intersecting knots in 4D infinite.^{[11] [ page needed ]} Because these surfaces are ii-dimensional, they tin form much more than complex knots than strings in 3D space tin. The Klein bottle is an example of such a knotted surface.^{[ citation needed ]} Another such surface is the real projective airplane.^{[ citation needed ]}

Hypersphere [edit]

The set of points in Euclidean four-space having the same distance R from a stock-still signal P₀ forms a hypersurface known as a 3-sphere. The hyper-volume of the enclosed space is:

${\displaystyle \mathbf {Five} ={\brainstorm{matrix}{\frac {i}{2}}\end{matrix}}\pi ^{two}R^{iv}}$

This is part of the Friedmann–Lemaître–Robertson–Walker metric in General relativity where R is substituted by part R(t) with t meaning the cosmological historic period of the universe. Growing or shrinking R with time means expanding or collapsing universe, depending on the mass density within.^[12]

Noesis [edit]

Research using virtual reality finds that humans, in spite of living in a iii-dimensional globe, tin, without special practice, make spatial judgments about line segments, embedded in four-dimensional space, based on their length (one dimensional) and the angle (two dimensional) between them.^[thirteen] The researchers noted that "the participants in our report had minimal practice in these tasks, and it remains an open question whether it is possible to obtain more sustainable, definitive, and richer 4D representations with increased perceptual experience in 4D virtual environments".^[13] In another study,^[fourteen] the ability of humans to orient themselves in 2D, 3D and 4D mazes has been tested. Each maze consisted of four path segments of random length and connected with orthogonal random bends, but without branches or loops (i.due east. actually labyrinths). The graphical interface was based on John McIntosh'due south gratuitous 4D Maze game.^[15] The participating persons had to navigate through the path and finally estimate the linear direction back to the starting point. The researchers found that some of the participants were able to mentally integrate their path later on some exercise in 4D (the lower-dimensional cases were for comparison and for the participants to learn the method).

Dimensional analogy [edit]

To sympathize the nature of four-dimensional infinite, a device called dimensional analogy is normally employed. Dimensional analogy is the study of how (northward − 1) dimensions relate to northward dimensions, and then inferring how due north dimensions would chronicle to (n + 1) dimensions.^[16]

Dimensional analogy was used by Edwin Abbott Abbott in the book Flatland, which narrates a story most a square that lives in a two-dimensional world, like the surface of a slice of newspaper. From the perspective of this foursquare, a iii-dimensional beingness has seemingly god-like powers, such as ability to remove objects from a rubber without breaking it open (by moving them across the third dimension), to see everything that from the 2-dimensional perspective is enclosed behind walls, and to remain completely invisible by standing a few inches abroad in the third dimension.

Past applying dimensional analogy, ane can infer that a 4-dimensional existence would be capable of like feats from the 3-dimensional perspective. Rudy Rucker illustrates this in his novel Spaceland, in which the protagonist encounters four-dimensional beings who demonstrate such powers.

Cross-sections [edit]

As a 3-dimensional object passes through a 2-dimensional plane, two-dimensional beings in this plane would only find a cross-section of the 3-dimensional object within this plane. For example, if a spherical balloon passed through a sheet of newspaper, beings in the newspaper would see first a single point, so a circle gradually growing larger, until it reaches the bore of the balloon, and and then getting smaller once more, until it shrank to a point and so disappeared. Information technology is important to remember that the 2d beings would non see a circle in the same way as nosotros do, rather merely a 1 dimensional projection of the circle on their 1D "retina". Similarly, if a iv-dimensional object passed through a three dimensional (hyper) surface, i could observe a iii-dimensional cantankerous-section of the four-dimensional object—for instance, a iii-sphere would appear get-go as a betoken, and then every bit a growing sphere, with the sphere then shrinking to a unmarried point and then disappearing.^[17] This ways of visualizing aspects of the time was used in the novel Flatland and also in several works of Charles Howard Hinton.^{[vi] : eleven–xiv} And in the same way iii dimensional beings (such as humans with a 2D retina) are unable to see a sphere in its entirety, in the same way equally 4D beings would with their 3D solid retina.

Projections [edit]

A useful application of dimensional analogy in visualizing higher dimensions is in projection. A projection is a way for representing an n-dimensional object in n − ane dimensions. For instance, reckoner screens are two-dimensional, and all the photographs of three-dimensional people, places and things are represented in 2 dimensions by projecting the objects onto a flat surface. By doing this, the dimension orthogonal to the screen (depth) is removed and replaced with indirect information. The retina of the eye is also a ii-dimensional assortment of receptors but the brain is able to perceive the nature of iii-dimensional objects by inference from indirect information (such equally shading, foreshortening, binocular vision, etc.). Artists often utilise perspective to give an illusion of three-dimensional depth to ii-dimensional pictures. The shadow, bandage by a fictitious grid model of a rotating tesseract on a airplane surface, as shown in the figures, is also the event of projections.

Similarly, objects in the time can be mathematically projected to the familiar three dimensions, where they can be more conveniently examined. In this case, the 'retina' of the 4-dimensional eye is a three-dimensional array of receptors. A hypothetical being with such an eye would perceive the nature of four-dimensional objects past inferring four-dimensional depth from indirect information in the three-dimensional images in its retina.

The perspective projection of three-dimensional objects into the retina of the heart introduces artifacts such as foreshortening, which the brain interprets every bit depth in the third dimension. In the same mode, perspective project from iv dimensions produces similar foreshortening effects. By applying dimensional analogy, one may infer four-dimensional "depth" from these effects.

Equally an analogy of this principle, the post-obit sequence of images compares various views of the three-dimensional cube with analogous projections of the four-dimensional tesseract into iii-dimensional space.

Cube	Tesseract	Description
		The image on the left is a cube viewed face-on. The analogous viewpoint of the tesseract in 4 dimensions is the prison cell-kickoff perspective projection, shown on the correct. I may draw an illustration between the two: just as the cube projects to a square, the tesseract projects to a cube. Note that the other v faces of the cube are not seen here. They are obscured by the visible face. Similarly, the other vii cells of the tesseract are non seen here because they are obscured by the visible prison cell.
		The image on the left shows the same cube viewed border-on. The analogous viewpoint of a tesseract is the face-first perspective projection, shown on the right. Just as the edge-first projection of the cube consists of two trapezoids, the face-showtime projection of the tesseract consists of 2 frustums. The nearest edge of the cube in this viewpoint is the one lying between the red and light-green faces. Also, the nearest face of the tesseract is the ane lying between the red and green cells.
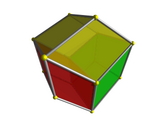		On the left is the cube viewed corner-starting time. This is analogous to the edge-commencement perspective projection of the tesseract, shown on the correct. Just as the cube'southward vertex-first projection consists of 3 deltoids surrounding a vertex, the tesseract's edge-showtime projection consists of 3 hexahedral volumes surrounding an border. Merely as the nearest vertex of the cube is the one where the three faces meet, so the nearest edge of the tesseract is the one in the middle of the projection book, where the three cells meet.
		A different analogy may be fatigued betwixt the edge-first projection of the tesseract and the edge-first project of the cube. The cube's edge-commencement projection has two trapezoids surrounding an edge, while the tesseract has three hexahedral volumes surrounding an border.
		On the left is the cube viewed corner-first. The vertex-first perspective projection of the tesseract is shown on the right. The cube'southward vertex-first project has three tetragons surrounding a vertex, only the tesseract'due south vertex-first projection has four hexahedral volumes surrounding a vertex. Just equally the nearest corner of the cube is the 1 lying at the middle of the image, so the nearest vertex of the tesseract lies not on boundary of the projected volume, merely at its center inside, where all four cells see. Note that just three faces of the cube'due south 6 faces tin can be seen hither, because the other 3 prevarication backside these three faces, on the opposite side of the cube. Similarly, just 4 of the tesseract'southward 8 cells can be seen here; the remaining 4 prevarication backside these 4 in the fourth direction, on the far side of the tesseract.

Shadows [edit]

A concept closely related to projection is the casting of shadows.

If a lite is shone on a iii-dimensional object, a two-dimensional shadow is cast. By dimensional analogy, light shone on a two-dimensional object in a two-dimensional world would cast a 1-dimensional shadow, and light on a one-dimensional object in a ane-dimensional world would bandage a zippo-dimensional shadow, that is, a betoken of non-lite. Going the other fashion, one may infer that light shone on a four-dimensional object in a iv-dimensional globe would cast a three-dimensional shadow.

If the wireframe of a cube is lit from higher up, the resulting shadow on a apartment 2-dimensional surface is a square within a foursquare with the corresponding corners connected. Similarly, if the wireframe of a tesseract were lit from "above" (in the fourth dimension), its shadow would be that of a iii-dimensional cube within another three-dimensional cube suspended in midair (a "apartment" surface from a four-dimensional perspective). (Note that, technically, the visual representation shown here is actually a two-dimensional paradigm of the three-dimensional shadow of the four-dimensional wireframe figure.)

Bounding volumes [edit]

Dimensional analogy also helps in inferring basic properties of objects in higher dimensions. For example, two-dimensional objects are bounded by ane-dimensional boundaries: a square is bounded past four edges. Three-dimensional objects are bounded past two-dimensional surfaces: a cube is divisional past 6 square faces. By applying dimensional illustration, one may infer that a 4-dimensional cube, known as a tesseract, is bounded past three-dimensional volumes. And indeed, this is the case: mathematics shows that the tesseract is divisional past 8 cubes. Knowing this is key to understanding how to interpret a iii-dimensional projection of the tesseract. The boundaries of the tesseract project to volumes in the image, not just 2-dimensional surfaces.

Visual telescopic [edit]

People have a spatial cocky-perception as beings in a three-dimensional space, but are visually restricted to ane dimension less: the middle sees the globe equally a projection to two dimensions, on the surface of the retina. Bold a four-dimensional being were able to encounter the earth in projections to a hypersurface, also just one dimension less, i.east., to 3 dimensions, it would be able to see, e.g., all 6 faces of an opaque box simultaneously, and in fact, what is inside the box at the same time, just every bit people can run into all 4 sides and simultaneously the interior of a rectangle on a piece of newspaper.^{[ citation needed ]} The beingness would be able to discern all points in a 3-dimensional subspace simultaneously, including the inner structure of solid three-dimensional objects, things obscured from human viewpoints in iii dimensions on two-dimensional projections. Brains receive images in two dimensions and use reasoning to help movie three-dimensional objects.

Limitations [edit]

Reasoning past analogy from familiar lower dimensions tin can be an excellent intuitive guide, merely care must be exercised non to accept results that are not more rigorously tested. For example, consider the formulas for the circumference of a circle: ${\displaystyle C=ii\pi r}$ and the surface area of a sphere: ${\displaystyle A=4\pi r^{two}}$ . One might gauge that the book of the unit of measurement 3-sphere in four-dimensional space is ${\displaystyle 5=6\pi r^{3}}$ , or possibly ${\displaystyle V=8\pi r^{3}}$ , only either of these would be wrong. The actual formula is ${\displaystyle V=2\pi ^{2}r^{3}}$ .^{[iv] : 119}

See likewise [edit]

• 4-polytope
• iv-manifold
• Exotic R ^iv
• 4-dimensionalism
• Fourth dimension in fine art
• Fourth dimension in literature
• List of iv-dimensional games
• Eugene the Jeep
• Time in physics
• Spacetime

References [edit]

1. ^ Cajori, Florian (1926), "Origins of Fourth dimension Concepts", The American Mathematical Monthly, 33 (eight): 397–406, doi:10.1080/00029890.1926.11986607
2. ^ Cajori, Florian (1926). "Origins of 4th Dimension Concepts" (PDF). The American Mathematical Monthly. 33 (8): 397–406. doi:x.1080/00029890.1926.11986607. JSTOR 2298325.
3. ^ Bong, Due east.T. (1965). Men of Mathematics (1st ed.). New York: Simon and Schuster. p. 154. ISBN978-0-671-62818-5.
4. ^ ^{a b c d} Coxeter, H.S.One thousand. (1973). Regular Polytopes (3rd ed.). New York: Dover Publishing. ISBN978-0-486-61480-9.
5. ^ Hinton, Charles Howard (1980). Rucker, Rudolf 5. B. (ed.). Speculations on the Time: Selected writings of Charles H. Hinton. New York: Dover. p. vii. ISBN978-0-486-23916-iii.
6. ^ ^{a b} Hinton, Charles Howard (1993) [1904]. The Quaternary Dimension. Pomeroy, Washington: Health Research. p. 14. ISBN978-0-7873-0410-2 . Retrieved 17 Feb 2017.
7. ^ Gardner, Martin (1975). Mathematical Carnival: From Penny Puzzles. Carte Shuffles and Tricks of Lightning Calculators to Roller Coaster Rides into the 4th Dimension (1st ed.). New York: Knopf. pp. 42, 52–53. ISBN978-0-394-49406-7.
8. ^ Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren
9. ^ Minkowski, Hermann (1909), "Raum und Zeit", Physikalische Zeitschrift, ten: 75–88
   • Various English translations on Wikisource: Infinite and Fourth dimension
10. ^ Møller, C. (1972). The Theory of Relativity (2nd ed.). Oxford: Clarendon Press. p. 93. ISBN978-0-19-851256-i.
11. ^ Carter, J.Scott; Saito, Masahico. Knotted Surfaces and Their Diagrams. American Mathematical Guild. ISBN978-0-8218-7491-two.
12. ^ D'Inverno, Ray (1998). Introducing Einstein's Relativity (Reprint ed.). Oxford: Clarendon Press. p. 319. ISBN978-0-nineteen-859653-0.
13. ^ ^{a b} Ambinder, Michael Southward.; Wang, Ranxiao Frances; Crowell, James A.; Francis, George K.; Brinkmann, Peter (October 2009). "Human iv-dimensional spatial intuition in virtual reality". Psychonomic Bulletin & Review. 16 (5): 818–823. doi:ten.3758/PBR.xvi.5.818. PMID 19815783.
14. ^ Aflalo, T. N.; Graziano, M. S. A. (2008). "4-dimensional spatial reasoning in humans" (PDF). Periodical of Experimental Psychology: Human being Perception and Performance. 34 (5): 1066–1077. CiteSeerX10.1.i.505.5736. doi:10.1037/0096-1523.34.five.1066. PMID 18823195. Retrieved twenty August 2020.
15. ^ "4D Maze Game". urticator.net. Retrieved 2016-12-16 .
16. ^ Kaku, Michio (1995). Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the Tenth Dimension (reissued ed.). Oxford: Oxford University Press. pp. Part I, Chapter 3. ISBN978-0-19-286189-4.
17. ^ Rucker, Rudy (1996). The Fourth Dimension: A Guided Bout of the Higher Universe. Boston: Houghton Mifflin. p. eighteen. ISBN978-0-395-39388-eight.

Further reading [edit]

• Archibald, R. C (1914). "Time every bit a Fourth Dimension" (PDF). Message of the American Mathematical Club: 409–412.
• Andrew Forsyth (1930) Geometry of Four Dimensions, link from Internet Archive.
• Gamow, George (1988). One Two Iii . . . Infinity: Facts and Speculations of Science (3rd ed.). Courier Dover Publications. p. 68. ISBN978-0-486-25664-1. Extract of folio 68
• E. H. Neville (1921) The Fourth dimension, Cambridge University Press, link from University of Michigan Historical Math Collection.

External links [edit]

• "Dimensions" videos, showing several different ways to visualize four dimensional objects
• Science News article summarizing the "Dimensions" videos, with clips
• Flatland: a Romance of Many Dimensions (second edition)
• Frame-past-frame animations of 4D - 3D analogies

rimmeralte1945.blogspot.com

Source: https://en.wikipedia.org/wiki/Four-dimensional_space

Share :